
La gravitation universelle, l’expansion de l’univers et la matière noire tirent leurs origines de la tension spatiale. Ces lois de la physique se manifestent sous forme d’accélération universelle par l’intermédiaire du flux de déplacement.
En connaissant la répartition de la masse visible dans l’univers, nous pouvons déterminer la densité spatiale en chaque point de l’univers. Une fois la densité spatiale déterminée à un instant t, nous pouvons suivre la dynamique de chaque corps qui se déplace dans l’univers.
Mais pour cela, il est nécessaire de comprendre la manière dont la densité spatiale est organisée en fonction de la masse visible.
L’étude de l’accélération des corps, pour des phénomènes physiques connus, me permet d’exprimer les densités spatiales. Ces cas particuliers m’informeront sur le lien entre la masse visible d’un corps et la densité spatiale induite.
Tout d’abord, exprimons la forme générale de la densité spatiale pour l’appliquer, par la suite, à des cas spécifiques tels que la gravitation, l’expansion de l’univers et la matière noire.
1.Accélération universelle et densité spatiale
Les relations
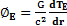 et
et
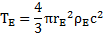 me permettent de définir une équation différentielle de l’accélération universelle ΦE que je présente ci-dessous :
me permettent de définir une équation différentielle de l’accélération universelle ΦE que je présente ci-dessous :
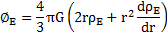
r est la position radiale qui a pour origine le point central de l’espace propre étudié
La résolution de cette équation différentielle me permet d’obtenir une expression générale de la densité spatiale :
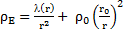 avec
avec
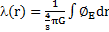
ρ0 et r0 sont des constantes
2.Gravitation universelle
Ce cas particulier m’a permis de définir la densité spatiale dans le cas d’un couple corps/espace propre isolé.
Soit un corps compact de masse mC, de rayon rC et de masse volumique ρC. Dans le cas de l’attraction d’un objet, qui se trouve dans l’espace propre à l’extérieur du corps compacte associé, le flux de déplacement est donné par l’accélération gravitationnelle qui est :
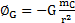
La résolution de l’équation différentielle, complétée par la condition ρE(rc) = ρC, permet de définir la densité spatiale. Dans le cas de la gravitation universelle, la densité spatiale a la forme suivante :
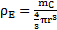
3.Expansion de l’univers
Je vais, en premier lieu, définir la densité spatiale afin d’exprimer la variable d’Hubble H. L’expression que je vais démontrer ci-dessous correspond à une solution de l’équation d’Einstein dans le cas de l’expansion de l’univers d’un espace sphérique.
Nous admettrons que le flux de déplacement qui caractérise l’expansion de l’univers, à notre époque, s’exprime selon l’expression suivante :
ΦH = H2.r. (r est la distance parcourue par le corps depuis le centre de l’univers)
Cette accélération a été déduite de la vitesse d’éloignement de 2 corps, séparés d’une distance d, exprimée par la loi d’Hubble : v = H.d.
La résolution de l’équation différentielle donne, dans le cas de l’expansion de l’univers, l’expression de la densité spatiale suivante :
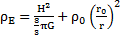
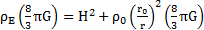
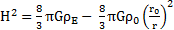
Or, à l’échelle de l’univers, ρE correspond à la répartition de la masse de l’univers dans son espace propre : donc ρE = ρU.
Dans l’espace propre de l’univers, ρE tend vers ρU lorsque r tend vers son rayon RU. De plus, nous avons démontré, dans la partie « IV. Relation entre grandeurs et constantes universelles », que :
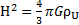
Si on se place dans les conditions limites (r=RU), alors :
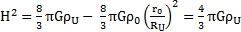
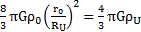
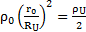
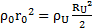
Cette condition limite me permet de déterminer :
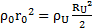
J’obtiens une expression de la variable d’Hubble H complètement définie :
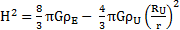
J’ai aussi démontré, dans la partie « IV. Relation entre grandeurs et constantes universelles », que
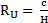 . De plus,
. De plus,
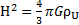 . J’en déduis que
. J’en déduis que
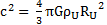 et donc :
et donc :
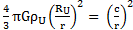
J’obtiens une nouvelle forme de la variable d’Hubble :
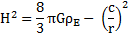
Cette relation est identique à l’une des solutions des équations d’Einstein dans le cas de l’expansion de l’univers :
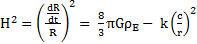
L’expression de la variable d’Hubble H trouvée dans cette étude correspond à la solution de la relativité générale dans le cas d’un univers de courbure sphérique.
4.Matière noire
Dans cette partie, je vais essayer de définir la répartition de la masse visible d’une partie d’une galaxie. En comparant avec les données expérimentales, nous pourrons confirmer ou infirmer le lien précis entre la masse visible et la densité spatiale. Je pense que l’étude des courbes de rotation, des galaxies et des amas de galaxies, peut nous conduire à mieux comprendre la répartition de la densité spatiale en fonction de la masse visible.
On se place dans le cas où la vitesse de rotation V0 d’une galaxie est constante. Le flux de déplacement, qui correspond à l’accélération centripète, s’exprime sous la forme suivante :
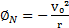
Pour ce cas, la résolution de l’équation différentielle nous donne l’expression de la densité spatiale ci-dessous :
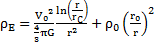
La densité spatiale ρE est définie par la distribution d’une forme d’énergie dans l’espace. Cette densité dépend de tous les corps qui se trouvent dans l’univers. Chaque corps matériel est associé à une énergie qui se répartit dans l’espace.
Dans le cas d’un corps isolé de masse mC et de centre de gravité 0, la densité qui se trouve à une distance r du centre 0 est donnée par la relation suivante :
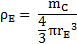
La répartition de la matière visible dans l’univers nous informe sur la distribution de la densité spatiale ρE et vice-versa.
Chaque corps Ci de masse mi apporte une densité d’énergie en chacun des points de l’espace. La somme des densités d’énergie de chacun de ces corps en un point M forme une densité spatiale locale.
Je suppose que la masse visible ΔmiV, qui se trouve dans le volume de la sphère de rayon r et d’épaisseur Δr, est répartie sous forme de densité spatiale de manière homogène dans la boule de rayon ri et d’origine le centre de l’espace propre étudié. Ce qui implique que la densité spatiale locale
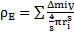
Soit mv(r) la masse visible d’une galaxie en fonction de la distance radiale r de son centre de gravité. Je définis sa masse volumique ρV(r) par la relation suivante :
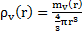
Alors la masse visible de la galaxie comprise dans le volume de la sphère de rayon r et d’épaisseur dr est : dmV(r) = ρV(r).4π.r2dr
Or
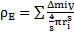
Je fais une approximation en exprimant cette relation sous la forme intégrale suivante :
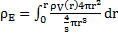
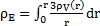
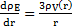
Nous pouvons donc exprimer la distribution de la densité de la matière visible à l’aide de la relation suivante :
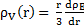 . Lorsque l’on étudie cette relation de manière plus approfondie, on remarque que les signes de ρV(r) et de ρE sont opposés. Par convention, nous prendrons ρE positive et V(r) négative.
. Lorsque l’on étudie cette relation de manière plus approfondie, on remarque que les signes de ρV(r) et de ρE sont opposés. Par convention, nous prendrons ρE positive et V(r) négative.
Cette expression me permet d’obtenir l’équation de la masse visible volumique suivante :
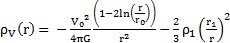
L’analyse des vitesses de rotation de diverses galaxies spirales me conduit à poser que r0 est le rayon de la galaxie RG. De plus, la condition limite
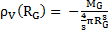 permet de déterminer l’expression de ρ1.r12. J’obtiens par conséquent :
permet de déterminer l’expression de ρ1.r12. J’obtiens par conséquent :
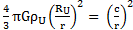
Ce qui me permet de déduire la forme de la masse visible volumique dans une galaxie :
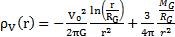
De plus
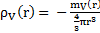 ,
j’obtiens donc la relation suivante :
,
j’obtiens donc la relation suivante :
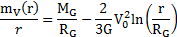
J’ai comparé la distribution de masse de cette expression avec celle de la masse baryonique relevée, laborieusement, sur les courbes de rotation de quelques galaxies spirales. Les distributions de masse sont identiques à un coefficient près de l’ordre de 1. Il faudrait aussi prendre en compte la masse des gaz, des poussières et de toutes les particules présentent dans une galaxie pour obtenir un résultat précis.
Par ailleurs, une simulation numérique nous permettrait de connaître la densité spatiale, précise en chaque point d’une galaxie, en fonction de la répartition de la masse visible. Ainsi nous pourrions déterminer précisément la vitesse de rotation des corps d’une galaxie sans l’intervention de la matière noire.
La tension superficielle spatiale permet d’unifier les lois de la cosmologie : gravitation universelle, expansion de l’univers et matière noire. Mais elle permet aussi de comprendre l’origine de l’équivalence masse-énergie.
5.Equivalence entre travail de la tension spatiale et E=mc2
J’ai précisé précédemment que la masse était le résultat d’une force au même titre que l’espace. Je vais calculer le travail effectué par la tension sur le rayon rc d’une particule de masse mc :
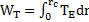
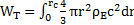
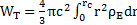
or
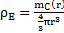
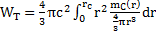
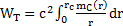
Si on suppose que la masse mc dans la particule est répartie de manière linéaire : mc(r) = µ.r avec µ constante. Alors le travail de la tension devient :
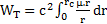
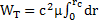
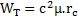
Or mc = mc(rc) = µ.rc, donc WT = c2 mc
On obtient finalement : WT = mc.c2
On retrouve la relation d’équivalence masse-énergie : E = m.c2.
L'énergie qui est contenue dans une masse correspond au travail de la tension superficielle spatiale effectué sur le rayon du corps
Auteur : Khalid Jerrari